La triangulation permet de calculer des distances dans des formes difficilement mesurables. Dans la vie courante, nous sommes amenés à effectuer des tas de mesures, diverses et variées. La mesure que probablement tout un chacun a déjà effectuée au moins une fois dans sa vie est celle mesure des distances. Qui n’a jamais mesuré sa taille?

Mesurer une distance demeure simple à effectuer sur des petites formes. Mais dès que les formes deviennent plus compliquées et grandes, cela devient de plus en plus compliqué. Comment peut-on mesurer par exemple la distance qui sépare Paris de Toulouse ?

La méthode de triangulation est justement utilisée pour mesurer, ou plutôt pour calculer des distances difficile à mesurer.

Un polygone est une figure géométrique plane qui possède de nombreux angles, c’est une ligne brisée à plusieurs endroits. Tous les polygones peuvent être décomposés en plusieurs triangles. Un carrée ou un rectangle peuvent être décomposés en 2 triangles rectangles, dans le cas du carrée les triangles sont rectangles et isocèles. Un pentagone en trois triangles, un hexagone en 4 triangles et ainsi de suite…

Principe de la triangulation

La décomposition d’une figure en plusieurs pièces de puzzle sous forme triangulaire s’appelle la triangulation. Le principe de la triangulation est la méthode utilisée par exemple en topographie pour cartographier une zone géographique.

Il est clair que maitriser la caractérisation des triangles permet de calculer les distances dans n’importe quel polygone. Il existe plusieurs règles qui permettent de calculer les différentes mesures des triangles.

Triangles rectangles

Les triangles rectangles sont des triangles qui possèdent un angle droit (un angle qui mesure 90°). Les règles de la trigonométrie s’appliquent à ce type de triangle. De ce fait on pourrait croire que les champs d’action de la trigonométrie est limité, car dans la nature on trouve beaucoup plus de triangles quelconques que de triangles droits, mais rassurez-vous, on peut trianguler un triangle…

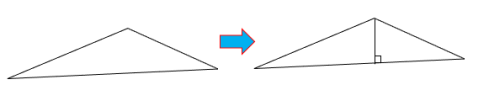
Comme pour les polygones, tous les triangles, peu importe leur nature, peuvent être décomposés en deux triangles rectangles, il suffit de tracer la droite perpendiculaire à l’un des côtés et passant par le sommet opposé à celui-ci.

Les formules de calcul dans le triangle

Il est donc important de savoir mesurer ou plutôt calculer les différentes dimensions d’un triangle. Il existe plusieurs théorèmes et règles qui permettent de lier les différentes dimensions d’un triangle entre elles. Parmi ces règles on peut citer par exemple La trigonométrie qui est justement la discipline qui permet de trouver les différentes mesures dans le triangle.

Théorème de Pythagore

L’un des théorèmes le plus célèbre et qui permet de calculer l’un des côtés d’un triangle rectangle à partir des deux autres côtés est le théorème de Pythagore. J’ai déjà publié un article qui détaille le théorème de Pythagore et sa réciproque.

Ce théorème s’applique aux triangles rectangles et permet de calculer l’hypoténuse à partir des deux côtés. Ces trois derniers paramètres sont des mesures de longueur. Les autres paramètres que l’on peut mesurer dans un triangle sont les angles. 

Règle des angles dans le triangle

Donc, un triangle peut être caractérisé par six paramètres au total : 3 longueurs et 3 angles

Le théorème de Pythagore lie les trois paramètres de longueur entre eux. Il existe aussi un théorème, ou une règle, qui permet de lier les angles d’un triangle. Voici l’énoncé de la règle des angles dans le triangle: «La somme des angles dans un triangle est égale à 180°».

On remarque que dans cette règle on ne spécifie pas la nature du triangle, celui-ci n’est pas obligé d’être droit. Mais dans le cas actuel, nous nous intéressons aux triangles rectangles.

Dans un triangle rectangle, un des trois angles mesure obligatoirement 90°, ce qui fait que la somme des deux autres angles égale à 90° (voir le schéma). 

Les deux angles dont la somme est égale à 90° s’appellent des angles complémentaires.

Rapports trigonométriques

Les rapports trigonométriques les plus souvent utilisés sont le sinus, le cosinus et la tangente. 

• Le sinus est le rapport trigonométrique qui se calcule en divisant le côté opposé (O) par l’hypoténuse (H) : sinus = O/H.
• Le cosinus est le rapport trigonométrique qui se calcule en divisant le côté adjacent (A) par l’hypoténuse : cosinus = A/H.
• La tangente est le rapport trigonométrique qui se calcule en divisant le côté opposé par adjacent : tangente = O/A.

Le théorème de Pythagore, la règle des angles dans un triangle et les rapports trigonométriques sont tous des techniques qui permettent de calculer une distance par triangulation. 

Tableau trigonométrique des angles particuliers 

Certains angles particuliers ont des rapports trigonométriques connus. Ou ils sont facile à calculer. Ces angles spécifiques sont : 0°, 30°, 45°, 60° et 90°.

Voici le tableau trigonométrique des angles particuliers :

Il est très facile à mémoriser les rapports trigonométriques des angles particuliers. Pour un angle quelconque on utilise une calculette. Les calculatrices scientifiques permettent de calculer les rapports trigonométriques de n’importe quel angle.

Comment calculer un angle

Nous avons vu jusqu’à présent comment peut-on utiliser les règles de la trigonométrie pour trouver les longueurs des côtés d’un triangle, et ce à partir seulement d’un angle et un des côtés du triangle rectangle. Mais il est tout à fait envisageable de tomber sur un cas où on connait seulement deux côtés du triangle rectangle.

En fait avec les deux côtés du triangle on peut calculer le troisième côté, en utilisant le théorème de Pythagore. Puis connaissant les trois côtés du triangle, il est donc possible de calculer les rapports trigonométriques.

Nous avons vu précédemment qu’à chaque angle correspond des rapports trigonométriques uniques. Il existe des fonctions inverses qui permettent de déterminer l’angle correspondant à chaque rapport trigonométrique. Ces fonctions s’appellent : arc-sinus, arc-cosinus et arc-tangente. Les calculatrices scientifiques sont dotées de fonctionnalités qui permettent de calculer un angle à partir de son sinus, cosinus ou tangente.

Calculatrice spécial collège :

La calculatrice pour le lycée

Lycée et supérieur

La triangulation est donc le fait de décomposer une forme géométrique quelconque en plusieurs triangles. Un triangle quelconque peut lui-même être décomposé en deux triangles rectangles. A partir du moment où la forme géométrique est triangulée, on peut utiliser l’une des règles citées ci-dessus pour calculer soit une distance ou bien un angle. Et on peut avancer ainsi, de triangle en triangle jusqu’à calculer l’ensemble de la forme géométrique.