A l’ère du numérique, il est rare de tomber dans une situation où on se retrouve obligé de tracer à la main le graphique d’une fonction affine. Et pourtant ce n’est guère compliqué pour apprendre à le faire, et surtout pour les fonctions simples telle que celle utilisée comme exemple dans l’article notion de fonction mathématique.

Voici les étapes qui permettent de tracer le graphique d’une fonction affine. Cette méthode marche aussi pour tracer le graphique d’une fonction linéaire.

Graphique d’une fonction affine. Axes des abscisses et ordonnées

Pour faire un graphique d’une fonction affine, la toute première étape consiste à tracer deux droites perpendiculaires. Et pour ce faire, on peut utiliser une feuille blanche et une règle, une feuille à carreaux ou encore une feuille millimétrée.

La droite horizontale sera la droite qui portera l’axe des abscisses. C’est sur cet axe qu’on retrouvera les valeurs de x (les antécédents).

Et la droite verticale portera l’axe des ordonnées. Et c’est sur cet axe qu’on retrouvera les images ou les valeurs de f(x).

Ces deux axes constituent le repère orthogonal dans lequel on pourra tracer le graphique d’une fonction affine.

Graduer les axes des abscisses et ordonnées

La deuxième étape consiste à graduer les deux axes, abscisses et ordonnées. Il faut diviser chaque axe en plusieurs graduations. Et il est très important que ces graduations aient la même taille. On peut utiliser pour cela une échelle adéquate.

On peut utiliser par exemple un tableau de valeurs de la fonction et essayer de trouver une échelle qui permet de faire apparaitre toutes les valeurs du tableau.

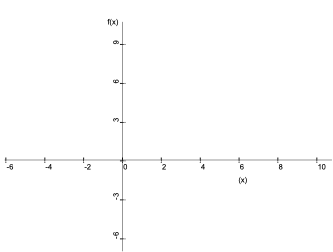
Voici un exemple de graduation. Chaque division de l’axe des abscisses vaut 2. Et chaque division de l’axe des ordonnées vaut 3.

Graphique d’une fonction affine, Les coordonnées d’un point

Ensuite, l’étape 3 consiste à positionner les points de construction du graphique. Ce sont des points qui appartiennent à la représentation graphique de la fonction.

Le couple abscisse et l’ordonnée qui lui correspond forme les coordonnées d’un point dans le repère orthogonal qu’on a construit précédemment.

En fait une représentation graphique d’une fonction est l’ensemble des points dont les coordonnées sont x et f(x).

Pour l’exemple de la fonction f(x) = x+2, on peut utiliser le tableau de valeur précédent et faire correspondre chaque couple d’abscisse, ordonnée à un point.

x	0	1	5	6,2	-6	-2
f(x)	2	3	7	8,2	-4	0
Points	A	B	C	D	E	F

Les points de construction du graphique

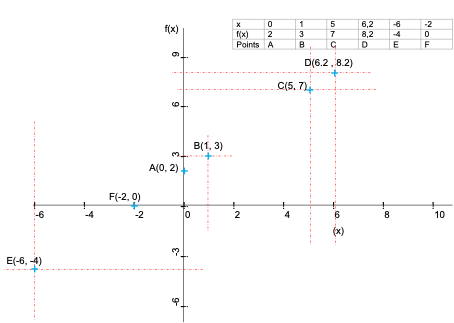
Les coordonnées du point A sont 0 et 2. On note A(0, 2)

Et de la même manière, les coordonnées du point B sont 1 et 3. On note B(1, 3). Ainsi de suite pour tous les autres points.

Pour tracer les points de construction du graphique, on utilise les coordonnées de chaque point pour le positionner dans le repère orthogonal. On obtient le point à l’intersection de la ligne verticale qui passe par l’abscisse, et la ligne horizontale qui passe par l’ordonnée. 

Voici la représentation qui correspond à la fonction f(x)=x+2 :

Tracer la représentation graphique de la fonction

En reliant tous les points de construction entre eux, on remarque qu’ils appartiennent à une ligne droite. Comme on peut le constater sur la construction graphique suivante

La fonction f(x) = x+2 est une fonction affine. Sa représentation graphique est une ligne droite qui ne passe pas par l’origine du repère, le point de coordonnées (0, 0).